



These are excerpts from a collection of graphical demonstrations I developed for first year calculus. I use many such demonstrations to illustrate and enrich my classes in the McAllister Technology Classroom. Those interested in higher math may also want to visit my page of graphics for complex analysis.
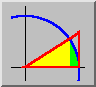
 Differentials and differences
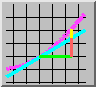
Differentials and differencesThis animation expands upon the classic calculus diagram above. The diagram illustrates the local accuracy of the tangent line approximation to a smooth curve, or--otherwise stated--the closeness of the differential of a function to the difference of function values due to a small increment of the independent variable. (In the diagram the increment of the independent variable is shown in green, the differential--i.e., the product of the derivative and the increment--in red, and the difference of function values as the red segment plus the yellow segment. The point is that if the green segment is small, the yellow segment is very small.) A problem with the diagram is that when it is drawn large enough to be visible the increment is too large to make the point. For example, here the yellow segment is about 30% of the green segment. This animation overcomes that problem by showing two views of the diagram, each changing as the increment varies. In the left view the ``camera'' is held fixed, and so the diagram becomes very small, while in the right view the ``camera'' zooms in so that the diagram occupies a constant area on the screen, and the relationship between the segment lengths can be clearly seen. Note how the yellow segment becomes very small in the second view (while the green segment appears to be of constant length due to the zoom). Note also that as we move in the difference between the purple curve and the blue tangent line becomes insignificant.
The MPEG animation requires about 168 KB. This gzipped Mathematica animation (15 KB) looks much better, but requires a Mathematica viewer. It was created with this Mathematica file. Some idea can be obtained by viewing a single frame.
 Computing the volume of water in a tipped glass
Computing the volume of water in a tipped glassThese images concern the computation of a volume by integrating cross-sectional areas. The first image reviews the basic principle. The other images treat a specific volume, that of the wedge of water formed when a cylindrical class of equal height and diameter is tipped until the water line runs through the center of the base. The pictures are frozen frames from AVS, and can only convey a rough idea of the interactive classroom presentation (which typically lasts about 30 minutes).
And now for the quiz: Compute the percentage of the glass filled by water using each of the the three slicings depicted in the last slide and verify that they all lead to the same answer.
 Archimedes' calculation of
Archimedes' calculation of 
In the third century B.C., Archimedes calculated the value of
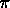 to an accuracy of one
part in a thousand. His technique was based on inscribing and
circumscribing polygons in a circle, and is very much akin to the method
of lower and upper sums used to define the Riemann integral. His
approach is presented in the following sequence of slides. If you have
an MPEG viewer with manual frame advance and sufficient memory, you can
view this seven frame (368 KB)
MPEG animation instead.
to an accuracy of one
part in a thousand. His technique was based on inscribing and
circumscribing polygons in a circle, and is very much akin to the method
of lower and upper sums used to define the Riemann integral. His
approach is presented in the following sequence of slides. If you have
an MPEG viewer with manual frame advance and sufficient memory, you can
view this seven frame (368 KB)
MPEG animation instead.
 How the ball bounces
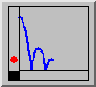
How the ball bouncesAs a way to help students appreciate functions, their applications, and their graphs, I involve them in a small project to describe the functions determined by the height of a bouncing ball. Although I start by dropping a real tennis ball from one meter above ground, a better quantitative idea of the function can be obtained from a computer animation, including a meter stick and clock. The students view the animation (in slow motion, with manual frame advance, etc.) and try to construct the graph of the function. As a homework assignment they are asked to determine the function algebraically. This is a piecewise quadratic and helps the students to realize that piecewise defined functions do exist outside of calculus books. Note: if you have a Mathematica viewer, select the Mathematica animations rather than the MPEG animations.
 Secants and tangents
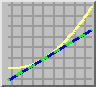
Secants and tangentsThis is a pretty straightforward animation depicting the geometric convergence of secant lines to the tangent line. I use various variations on this demo during the early part of a calculus course, of which three are shown here. Note: if you have a Mathematica viewer, select the Mathematica animations rather than the MPEG animations.
 Zooming in on a tangent line
Zooming in on a tangent lineThis is a version of the common demonstration that a smooth curve is indistiguishable from its tangent line when viewed under a sufficiently high power microscope. Students can easily demonstrate this themselves using a graphics calculator equipped with a zoom button. In this animation, we provide some extra distance queueing by showing the grid and striping the tangent line. Note: if you have a Mathematica viewer, select the Mathematica animation rather than the MPEG animation.
 A
trigonometric limit
A
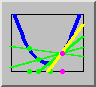
trigonometric limitAn elegant geometric proof which is well within the reach of a beginning calculus student is the proof of the fundamental trigonometric limit
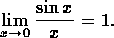
The proof is based on a diagram depicting a circular sector in the unit circle together with an inscribed and a circumscribed triangle. From the fact that the sector has area exceeding that of the inscribed triangle but less than that of the circumscribed one is lead to the inequalities
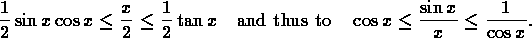
The proof then follows from the "squeeze theorem."
I usually spend about 15 minutes on this proof, including lots of class participation. The diagram is built up in three steps: first the sector only, then with the inscribed triangle, and finally with both triangles. Here are some instructions for creating it in class. During the presentation I make frequent recourse to plotting software to verify the various inequalities. For example this plot, constructed from this MATLAB file, convincingly verifies the second set of inequalities.
 The limit
The limitThese are some simple graphs which are useful in a discussion of limits. The first three functions all have limit -5 as x approaches 1, emphasizing the irrelevance of the value of the function at the limit point itself. The last function has different left and right hand limits at 1, and so the limit does not exist. The graphs were constructed with this MATLAB file.
 A nowhere differentiable function
A nowhere differentiable functionA brief graphical exploration of a continuous, nowhere differentiable function fits very well in the first semester of calculus, for example, to provide a strong counterexample to the converse of the theorem that differentiability implies continuity; or to show that it is only differentiable functions which look like straight lines under the microscope. Given good classroom graphics facilities such an exploration is easy, but it is almost hopeless without them. This plot of such a function was produced with a few lines of Matlab code following Weierstrass's classical construction. In class I zoom in on this graph several times to reveal its fractal nature. Consequently I used a very fine point spacing. On a slower machine it is preferable to use fewer points, and decrease the point spacing as you zoom in.
 2.718281828459045235360287471352662
2.718281828459045235360287471352662
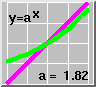
Students are often very puzzled by the appearance of the number e,
which is given above (to 35 decimal places). A simple explanation of
its origin arises from the fact that e is the only number for
which the tangent to the graph of 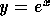 through the point (0,1) has slope exactly 1. The important result
that the function
through the point (0,1) has slope exactly 1. The important result
that the function 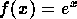 is its own derivative follows easily from this fact and the elementary
laws of exponents. The Mathematica animations here simply show the
graph of
is its own derivative follows easily from this fact and the elementary
laws of exponents. The Mathematica animations here simply show the
graph of 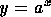 ,
but with varying a. By manipulating the frame advance, the
instructor can adjust a so that the tangent has slope close to
1. The second animation is similar to the first, but drawn on a larger
scale, and from it one can read off the first few decimal places of e.
Note: if you have a Mathematica viewer, select the Mathematica
animations rather than the MPEG animations.
,
but with varying a. By manipulating the frame advance, the
instructor can adjust a so that the tangent has slope close to
1. The second animation is similar to the first, but drawn on a larger
scale, and from it one can read off the first few decimal places of e.
Note: if you have a Mathematica viewer, select the Mathematica
animations rather than the MPEG animations.
 The intersection of two cylinders
The intersection of two cylindersHere's a demonstration by my colleague David Sibley illustrating the computation of the volume of the region formed by two intersecting cylinders.
 This
work is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.
This
work is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.