The picture on the left shows a graph of

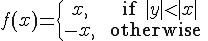
The red line shows the cross section x=0, while the green line highlights the cross section y=0. Click and drag on the picture to rotate it; type "F" after clicking on the picture to view the cross sections without the surrounding surface.¹

For this function,

• f_y(0,0)=0; it's the slope of the line tangent to the red curve at the point of intersection.
• f_x(0,0)=1; when y=0, we have f(x,y)=f(x,0)=x, and the derivative of this function with respect to x is 1, whether we're at the origin or anywhere else along the line.

Both of the partials exist at the origin, but the function clearly is not differentiable at (0,0); if the surface had a tangent plane there it would simultaneously have to be both z=x and z=-x.

Most calculus books include a theorem saying that if the partials are continuous at and around a point, a function is differentiable. The reason this example doesn't contradict the theorem is that the partials are not continuous at the origin.

However, it's also possible that a function is differentiable with discontinuous partials.